WPF实现Win32API的调用

发表于 2020-09-10 更新于 2020-09-15 分类于 .NET Disqus：
本文字数： 427 阅读时长 ≈ 1 分钟
博客园同步已开启

之前在暑假的时候学了FDU的SoC课程，故对编译时的情况有了一定的了解。在WPF当中，如果我们要调用Win32API（这里以keybd_event为例）：

1 2	[DllImport("user32.dll", EntryPoint = "keybd_event", SetLastError = true)] public static extern void keybd_event(byte bVk, byte bScan, uint dwFlags, uint dwExtraInfo);

上述代码的意思也显而易见，DllImport是一个attribute标签。值得注意的是下面的extern关键词。众所周知，.dll的全称是Dynamic Link Library，即在编译时编译器会根据代码中的声明对库中的方法动态链接。这里的extern即，是对keybd_event做了声明，并明确是在user32.dll当中。其他Win32API的调用同理。

WPF实现系统托盘

发表于 2020-09-10 更新于 2020-09-15 分类于 .NET Disqus：
本文字数： 3.1k 阅读时长 ≈ 3 分钟
博客园同步已开启

在WinForm当中，我们可以使用非常轻松地实现系统托盘，在.NET Core的WPF当中，System.Windows.Form并不能作为命名空间引用，本文将讲述如何在WPF中实现系统托盘，以及如何将窗口最小化到系统托盘。

安装NuGet包

搜索Hardcodet.NotifyIcon.Wpf并安装：

编写ViewModel

public class NotifyIconViewModel
{
    /// <summary>
    /// 激活窗口
    /// </summary>
    public ICommand ShowWindowCommand
    {
        get
        {
            return new DelegateCommand
            {
                CommandAction = () =>
                {
                    Application.Current.MainWindow.Activate();
                }
            };
        }
    }

    /// <summary>
    /// 隐藏窗口
    /// </summary>
    public ICommand HideWindowCommand
    {
        get
        {
            return new DelegateCommand
            {
                CommandAction = () => Application.Current.MainWindow.Hide()
            };
        }
    }


    /// <summary>
    /// 关闭软件
    /// </summary>
    public ICommand ExitApplicationCommand
    {
        get
        {
            return new DelegateCommand { CommandAction = () => Application.Current.Shutdown() };
        }
    }
}

其中，虽然代码中用到了DelegateCommand类，但实际上并未实际发生作用，只是为了更好地封装代码，增加某些特定条件下的可读性，读者也可自行将其更改为普通的Command。下面为DelegateCommand类代码：

public class DelegateCommand : ICommand
{
    public Action CommandAction { get; set; }
    public Func<bool> CanExecuteFunc { get; set; }

    public void Execute(object parameter)
    {
        CommandAction();
    }

    public bool CanExecute(object parameter)
    {
        return CanExecuteFunc == null || CanExecuteFunc();
    }

    public event EventHandler CanExecuteChanged
    {
        add { CommandManager.RequerySuggested += value; }
        remove { CommandManager.RequerySuggested -= value; }
    }
}

在App.xaml中添加托盘信息并关联ViewModel

在App.xaml添加命名空间：

1	xmlns:tb="http://www.hardcodet.net/taskbar"

如果策略并不是隐藏窗口而是直接关闭窗口，那么为了防止所有窗口都退出导致的程序关闭，我们需要添加额外的一行属性：

1	ShutdownMode="OnExplicitShutdown"

而不是原来的OnLastWindowClose。接下来，我们在Application.Resource标签内添加系统托盘：

<Application.Resources>
    <ContextMenu x:Shared="false" x:Key="SysTrayMenu">
        <MenuItem Header="显示窗口" Command="{Binding ShowWindowCommand}" />
        <MenuItem Header="关闭窗口" Command="{Binding HideWindowCommand}" />
        <Separator />
        <MenuItem Header="退出" Command="{Binding ExitApplicationCommand}" />
    </ContextMenu>
    <tb:TaskbarIcon x:Key="Taskbar"
                    ToolTipText="UIToy by Haoyun Qin"
                    DoubleClickCommand="{Binding ShowWindowCommand}"
                    ContextMenu="{StaticResource SysTrayMenu}"
                    IconSource="UIToy.ico">
        <tb:TaskbarIcon.DataContext>
            <local:NotifyIconViewModel />
        </tb:TaskbarIcon.DataContext>
    </tb:TaskbarIcon>
</Application.Resources>

上面，我们针对不同的操作，绑定了相关的命令。还需要添加一个ico文件（这里我添加的是UIToy.ico）

在启动时显示系统托盘

在App.xaml.cs当中初始化Taskbar：

public partial class App : Application
{
    public static TaskbarIcon TaskbarIcon;

    protected override void OnStartup(StartupEventArgs e)
    {
        base.OnStartup(e);
        TaskbarIcon = (TaskbarIcon)FindResource("Taskbar");

    }
}

然后我们就可以发现，图标已经在系统托盘当中显示了。

20年OI刷题(1) - 归并排序

发表于 2020-09-04 更新于 2020-09-15 分类于 OI Disqus：
本文字数： 1.1k 阅读时长 ≈ 1 分钟
博客园同步已开启

原理

不做赘述，细看下图：

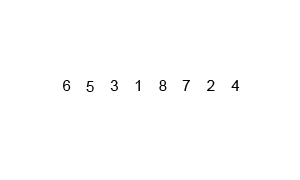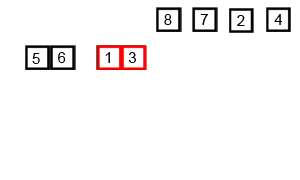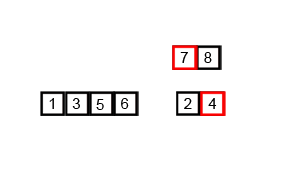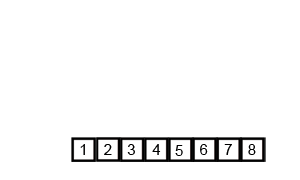
复杂度

时间复杂度：$O(n\log n)$
空间复杂度：$O(n)$

代码

（码风不好看，不喜勿碰）

#include <iostream>

using namespace std;

const int MAXN = 100005;

int n;
int a[MAXN], temp[MAXN];

template<typename T>
void merge_sort(T arr, T temp, int l, int r) {
    if (l >= r) return;
    int mid = (l + r) >> 1;
    merge_sort(arr, temp, l, mid);
    merge_sort(arr, temp, mid + 1, r);
    int i = l, j = mid + 1, k = l;
    while (i <= mid && j <= r)
        temp[k ++] = arr[i] < arr[j] ? arr[i ++] : arr[j ++];
    while (i <= mid)
        temp[k ++] = arr[i ++];
    while (j <= r)
        temp[k ++] = arr[j ++];
    for (register int i = l; i <= r; i ++) arr[i] = temp[i];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    merge_sort(a, temp, 1, n);
    for (int i = 1; i <= n; i ++) cout << a[i] << " ";
    cout << endl;
    return 0;
}

当然了，你也可以：

#include <iostream>
#include <algorithm>

using namespace std;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    sort(a + 1, a + 1 + n);
    for (int i = 1; i <= n; i ++) cout << a[i] << " ";
    cout << endl;
    return 0;
}

测试传送门

https://www.luogu.com.cn/problem/P1177

代码下载

Download

累。

发表于 2020-09-04 更新于 2020-09-11 分类于随想 Disqus：
本文字数： 15 阅读时长 ≈ 1 分钟

当热情散退之后，世界空无一物。

VBA实现日期自动标记以及表格数据更新

发表于 2020-09-02 更新于 2020-09-15 分类于 VBA Disqus：
本文字数： 2.4k 阅读时长 ≈ 2 分钟
博客园同步已开启

需求

自动标记当前日期所在的列，高亮
自动更新图标数据源

实现

使用ActiveX控件实现

'Get English Name of Column
Public Function Fun_GetEngName(ByVal argColumn As Integer) As String
    Dim strEngName As String
    Dim iNum, iMod As Integer

    iNum = argColumn \ 26
    iMod = argColumn Mod 26
    If (iMod = 0) Then
        If (iNum = 1) Then
            strEngName = Chr(90)
        Else
            strEngName = Chr(65 + iNum - 2) + Chr(90)
        End If
    Else
        If (iNum = 0) Then
            strEngName = Chr(65 + iMod - 1)
        Else
            strEngName = Chr(65 + iNum - 1) + Chr(65 + iMod - 1)
        End If
    End If
    Fun_GetEngName = strEngName
End Function

Private Sub CommandButton1_Click()
    'Clear Background Color
    Rows("1:1").Interior.ColorIndex = 2
    Rows("2:2").Interior.ColorIndex = 2
    'Get Current Date
    Dim idate As Date
    idate = Format(Now, "yyyy/m/d")
    MsgBox "Today is " & idate & ", have a nice day!", , "Auto Dater, by H.Q."
    'Set the bgcolor of the cell of current date
    Worksheets(1).Cells(171, 3).Value = idate
    Dim i
    i = Worksheets(1).Cells(171, 5).Value
    Worksheets(1).Cells(2, i).Interior.ColorIndex = 8
    Worksheets(1).Cells(1, i).Interior.ColorIndex = 8
    'Set data source of charts (till yesterday)
    Dim s As String
    s = Fun_GetEngName(i - 1)
    ActiveSheet.ChartObjects("TimingStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$107:$" & s & "$111")
    ActiveSheet.ChartObjects("SleepingStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$107:$" & s & "$107")
    ActiveSheet.ChartObjects("EntertainmentStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$110:$" & s & "$110")
    ActiveSheet.ChartObjects("StudyStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$108:$" & s & "$108")
    ActiveSheet.ChartObjects("NormalStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$109:$" & s & "$109")
    ActiveSheet.ChartObjects("TechStatistics").Activate
    ActiveChart.SetSourceData Source:=Range("Main!$A$2:$" & s & "$2,Main!$A$111:$" & s & "$111")
End Sub

注意事项

图表名称需要命名，具体方法：https://www.xuexila.com/excel/biaoge/1647271.html
日期的减法时使用Excel内置函数的-实现的

效果

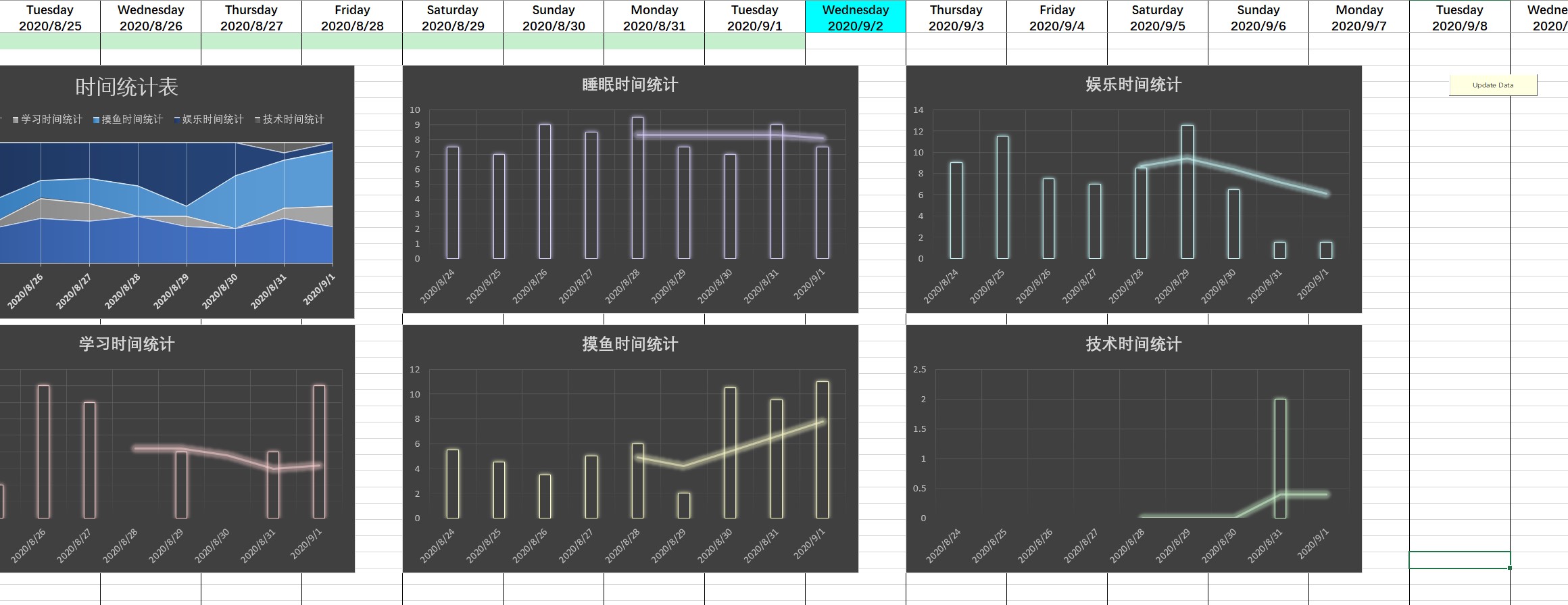
关于内网穿透

发表于 2020-08-21 更新于 2020-09-15 分类于网络 Disqus：
本文字数： 528 阅读时长 ≈ 1 分钟
博客园同步已开启

于2020年5月就已实现此功能，特此记录。

设备列表

中国电信SDN网关
小米AIoT路由器 AX3600

基本原理

由于在广域网上是无法直接访问家里局域网的设备的，所以我们需要将我们局域网当中的设备映射到公网IP（光猫）的某些端口上，一般有两种方式实现：

DMZ虚拟主机
端口转发

由于我们家里到我电脑经过了二级路由，我才用了在二级路由（小米路由器）上进行端口转发，然后直接将路由器的所有端口都映射到光猫上（DMZ虚拟主机）

配置过程

在浏览器中输入路由器的IP地址（或者小米路由器可以输入miwifi.com）进入配置页面，输入WiFi密码登陆：

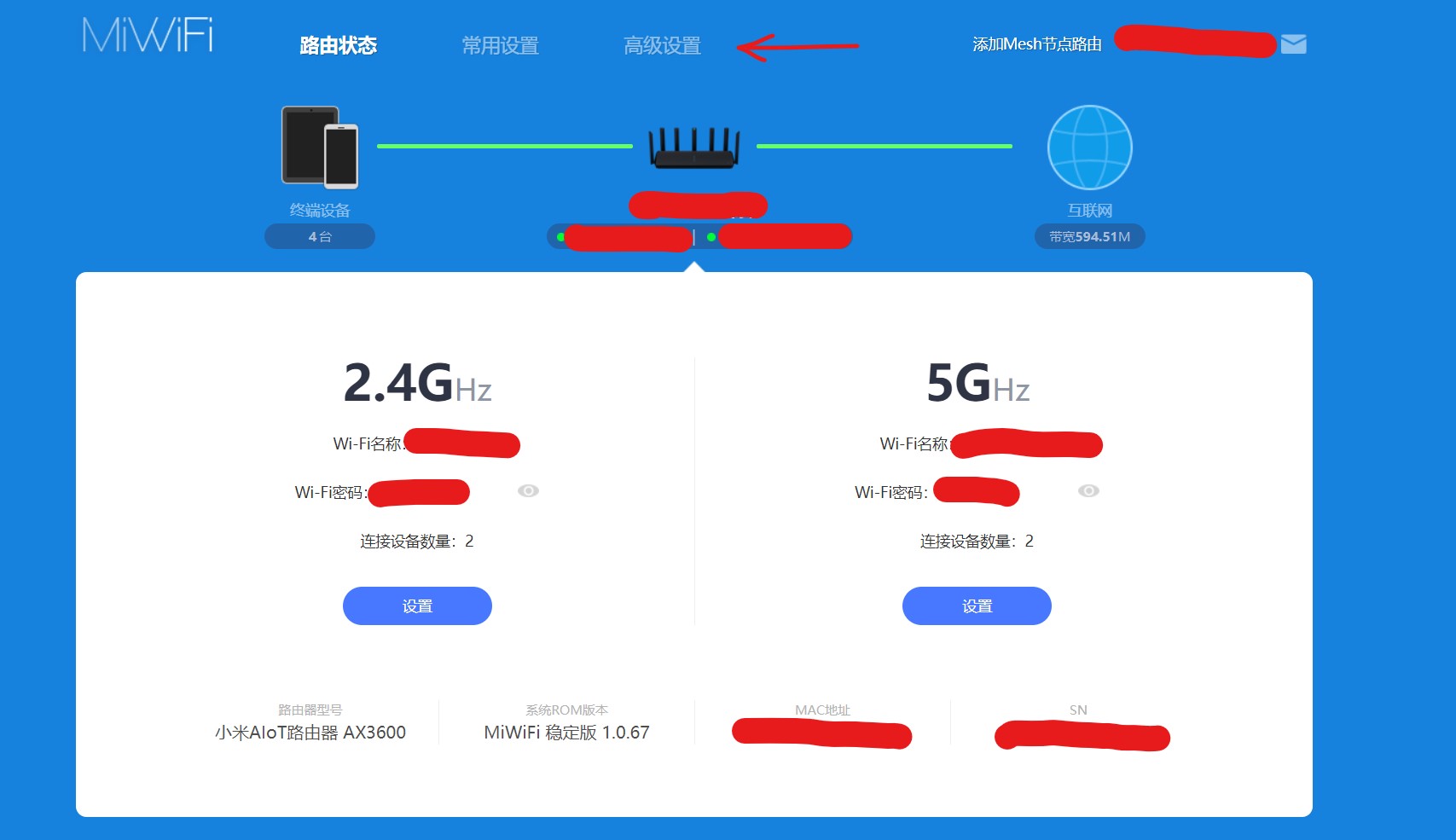
接下来进入高级设置，设置端口转发。参数意义如下：

名称：随意
协议：即支持的协议类型，建议TCP/UDP
外部端口：即映射到路由器上的端口
内部IP地址：你要做穿透的计算机主机IP地址
内部端口：计算机服务端口

配置完毕之后，进入SDN网关的App（网络管家）进行操作，打开DMZ虚拟主机功能，并将IP地址设置为路由器IP地址。

常见端口

8888：Jupyter Notebook的端口
3389：Remote Desktop Protocol
4000：Hexo

注意事项

尽量不要将外部端口设为一些常用端口，更不能设置成80这样的端口（当心网警找上门）

对RCF网络的理解

发表于 2020-08-20 更新于 2020-09-22 分类于深度学习 Disqus：
本文字数： 1.3k 阅读时长 ≈ 1 分钟
博客园同步已开启

原论文

原论文：
https://mmcheng.net/rcfEdge/

网络架构

下图为RCF网络架构：

RCF网络架构

其建立在VGG16之上，根据其修改而来。与原来的VGG16相比：

RCF网络去除了原来所有的全连接层（最后的三个全连接层）以及最后的池化层。这样做是因为与VGG网络的设计初衷——图像分类问题不同，这个网络旨在边缘检测，VGG最后的全连接层得到的$1 \times 1 \times 4096$的输出是没有意义的，所以将其删去。
为了进行边缘信息的提取，所以需要对像素值本身进行重新计算，所以在VGG16的每个卷积层后，都添加了一个$1\times 1 - 21$的卷积层，先升维，后通过$1 \times 1 - 1$进行降维。
其在每一个stage的最后添加了cross-entropy loss / sigmoid层以计算损失，更新参数。
每一层中有deconv层进行上采样，将图像大小映射回原来的大小，最后在fusion部分将每一个stage的输出叠加，在进行一遍$1\times 1 - 1$的卷积将多通道合并，来达到获取多种混合信息的能力。

损失函数

由于数据集通常是由多个标记者 (Annotator) 标记的。虽然每个人的认知不同，但是大家的结果都具有很高的一致性。对于每一张图片，我们将所有人的标记取平均值来生成一个边缘存在的概率图。对于每一个点，$0$代表没有标记者认为这个点是边缘，$1$则代表所有人都认为这个点是边缘。这里定义一个超参数$\eta$：如果一个点是边缘的概率大于$\eta$，则这个点我们认为其是边缘；若这个点的概率是$ 0 $，则其不是边缘；此外，认为那些概率介于$ 0 $和$ \eta $之间的点是属于有争议的点，不计入损失函数。所以，每一个点的损失函数可以记为：

$l(X_i; W) = \begin{cases} \alpha \cdot \log (1 - P(X_i; W)) & \text {if } y_i = 0 \\ 0 & \text {if } 0 < y_i \leq \eta \\ \beta \cdot \log P(X_i; W) & \text {otherwise}, \end{cases}$

其中，

$\alpha = \lambda \cdot \frac {|Y^+|} {|Y^+| + |Y^-|}$ $\beta = \cdot \frac {|Y^-|} {|Y^+| + |Y^-|}$

$|Y^+|$表示图中一定是边缘的点的个数，$|Y^-|$表示图中一定不是边缘的点的个数，$\lambda$则是超参数。在像素$i$的特征向量和是否为边缘的事实表示分别为$X_i$和$y_i$，$P(X)$是一个标准的Sigmoid激活函数，$W$则代表网络中的所有学习参数。所以，整个图片的损失函数可以记为：

$L(W) = \sum _ {i = 1} ^ {|I|} \Big ( \sum _ {k = 1} ^ K l(X_i ^ {(k)}; W) + l(X_i ^ {\text {fuse}}; W)\Big )$

其中，$X_i ^ {(k)}$表示stage k的特征向量，$X_i ^ \text {fuse}$表示stage fusion的特征向量，$|I|$代表像素个数，$|K|$代表阶段数（此处为5）

Online Demo

https://mc.nankai.edu.cn/edge

对SRAM中Stack的理解

发表于 2020-08-20 更新于 2020-09-15 分类于 SoC Disqus：
本文字数： 854 阅读时长 ≈ 1 分钟
博客园同步已开启

在七月份学习SoC的时候，教授谈到了SRAM中的stack部分。当时上课的时候，教授让我猜这到底是干什么的，我当时说可能是存放临时变量的地方，真没想到是真的。

下图是M2e芯片对地址的索引：

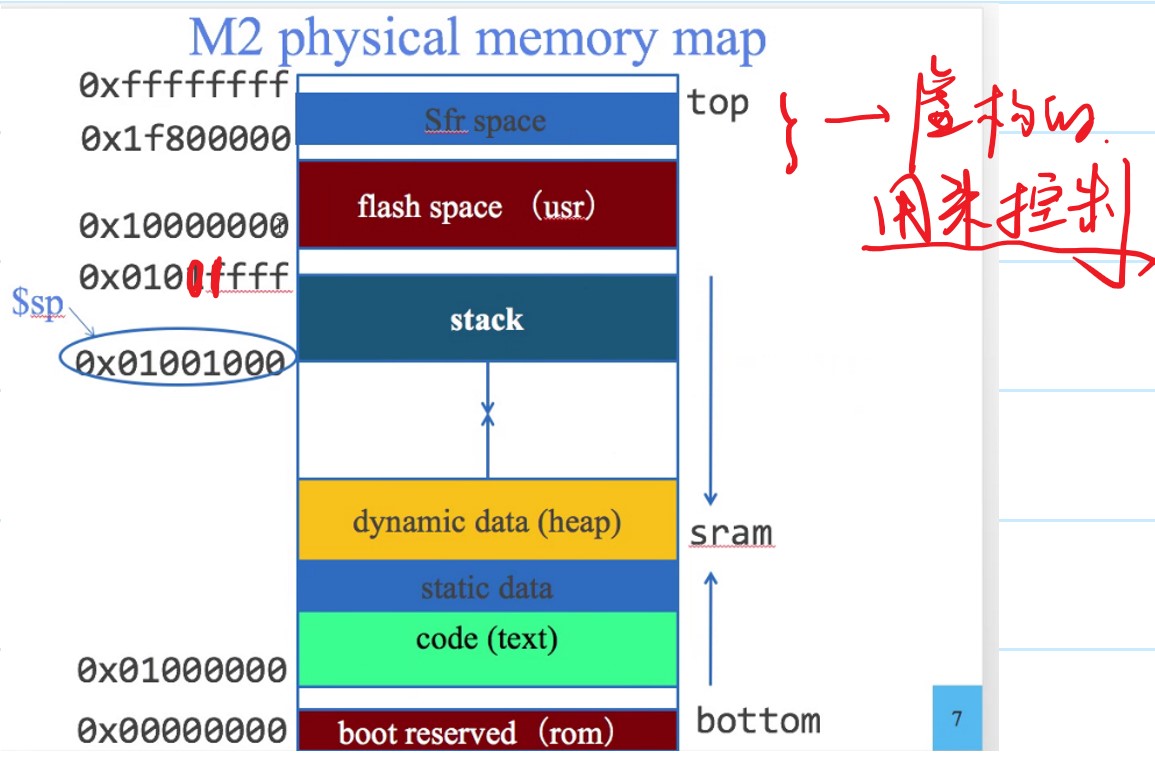
stack其实就是栈，是一种LIFO的数据结构。一开始写汇编的时候可能没什么感觉，但是当汇编写多了，使用到了子程序（submodule）以后就会发现，stack其实是有作用的。先扯一点关系不大的事情。在最开始学习寄存器的时候，我们会发现那张表上面有一个saved registers和temporary register。如果只用汇编的话，我们会发现混起来用一点关系都没有，因为我们其实只是在操作寄存器。然而，当我们在使用C和汇编混编的时候就会发现端倪。temporary寄存器是在函数跳转之后不被保存的寄存器，然而save寄存器则是在函数跳转之后还被保存的寄存器。这里我们谈到的“保存”其实就是和stack有关的操作。如果我们要保存一个32位的数，那我们其实只需要将stack pointer（sp）减去4，然后把值放在sp的位置，要取回的时候再加上四。注意：stack pointer的操作在自己的子程序当中一定要对称，即进来的时候sp是多少，出去的时候sp还是多少。其实这里的stack就是我们手动实现的，stack pointer就是栈顶指针罢了。接下来，我举一个例子：

C语言中正在执行一个void，叫做a()，a()调用了汇编中的子程序b()，那么在调用b之前，如果运行的时候save寄存器中有东西，那就C编译器编译时就会有若干条指令来吧这些寄存器当中的值压回stack当中，并不会管temporary寄存器当中的值（因为一般来说C的编译器只有在使用临时变量是会使用$t*。接下来，进入b子程序之后，如果b子程序要调用C的一个子程序c()，那么在汇编当中，上述的保存过程就要手动实现了。

总之，对于MIPS而言，他就是一个load-and-store structure，一切都可以通过操作寄存器、储存，使用ALU运算完成。

VGG网络可以支持任意尺寸的理解

发表于 2020-08-20 更新于 2020-09-15 分类于深度学习 Disqus：
本文字数： 1.6k 阅读时长 ≈ 1 分钟
博客园同步已开启

原论文：

Very Deep Convolutional Networks for Large-Scale Image Recognition

arXiv：[1409.1556] Very Deep Convolutional Networks for Large-Scale Image Recognition

intro：ICLR 2015

homepage：Visual Geometry Group Home Page

下图为VGG网络的网络结构

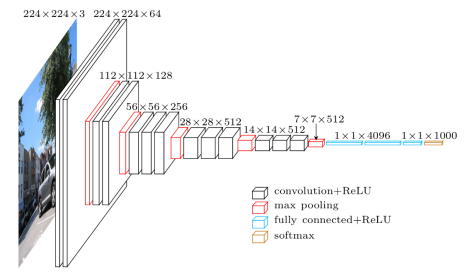
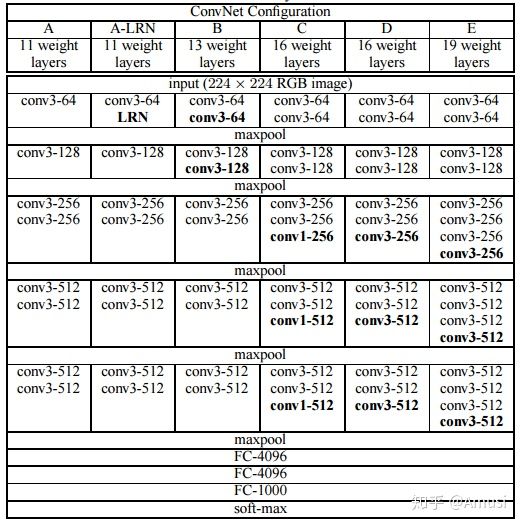
在这里我就不多赘述为什么要用小卷积核，小卷积核有什么好处，感受野，等等，诸如此类问题。这些东西网上讲解的非常详尽。我这里主要想探讨一下关于VGG可以接受任意大小的图片的原因。

众所周知，卷积层和池化层不会对长宽有着硬性规定。因为卷积层迭代的其实就是卷积核当中的参数，与输入做卷积运算，不会有什么影响。注意到最后的全连接层。全连接层其实是可以和卷积层互换的，而且他们的参数规模都是一样的。具体原因，可以看下面这篇文章：

https://blog.csdn.net/jyy555555/article/details/80515562

引用：

上图是VGG网络最后三层的替换过程，上半部分是训练阶段，此时最后三层都是全连接层（输出分别是4096、4096、1000），下半部分是测试阶段（输出分别是1x1x4096、1x1x4096、1x1x1000），最后三层都是卷积层。下面我们来看一下详细的转换过程（以下过程都没有考虑bias，略了）：

先看训练阶段，有4096个输出的全连接层FC6的输入是一个7x7x512的feature map，因为全连接层的缘故，不需要考虑局部性，可以把7x7x512看成一个整体，25508（=7x7x512）个输入的每个元素都会与输出的每个元素（或者说是神经元）产生连接，所以每个输入都会有4096个系数对应4096个输出，所以网络的参数（也就是两层之间连线的个数，也就是每个输入元素的系数个数）规模就是7x7x512x4096。对于FC7，输入是4096个，输出是4096个，因为每个输入都会和输出相连，即每个输出都有4096条连线（系数），那么4096个输入总共有4096x4096条连线（系数），最后一个FC8计算方式一样，略。

再看测试阶段，由于换成了卷积，第一个卷积后要得到4096（或者说是1x1x4096）的输出，那么就要对输入的7x7x512的feature map的宽高（即width、height维度）进行降维，同时对深度（即Channel/depth维度）进行升维。要把7x7降维到1x1，那么干脆直接一点，就用7x7的卷积核就行，另外深度层级的升维，因为7x7的卷积把宽高降到1x1，那么刚好就升高到4096就好了，最后得到了1x1x4096的feature map。这其中卷积的参数量上，把7x7x512看做一组卷积参数，因为该层的输出是4096，那么相当于要有4096组这样7x7x512的卷积参数，那么总共的卷积参数量就是：

[7x7x512]x4096，这里将7x7x512用中括号括起来，目的是把这看成是一组，就不会懵。

第二个卷积依旧得到1x1x4096的输出，因为输入也是1x1x4096，三个维度（宽、高、深）都没变化，可以很快计算出这层的卷积的卷积核大小也是1x1，而且，通道数也是4096，因为对于输入来说，1x1x4096是一组卷积参数，即一个完整的filter，那么考虑所有4096个输出的情况下，卷积参数的规模就是[1x1x4096]x4096。第三个卷积的计算一样，略。

其实VGG的作者把训练阶段的全连接替换为卷积是参考了OverFeat的工作，如下图是OverFeat将全连接换成卷积后，带来可以处理任意分辨率（在整张图）上计算卷积，而无需对原图resize的优势。

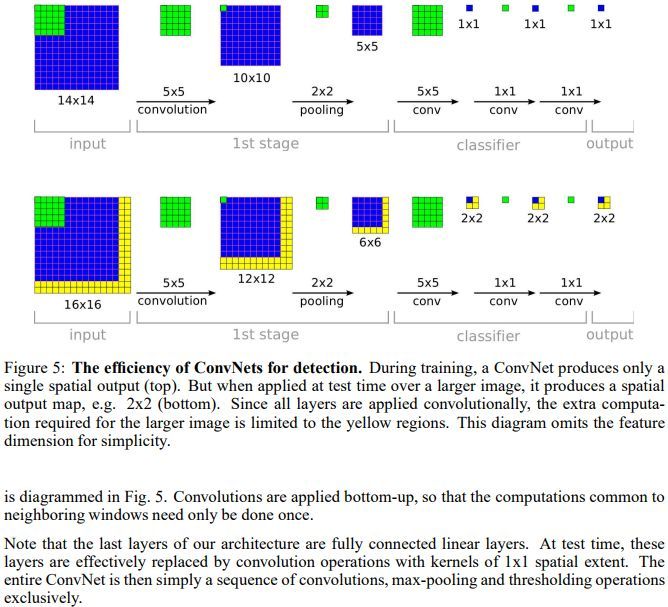
Digression：前段时间看了RCF网络，他之所以可以输出和输入同样尺寸的图片，就是因为其只有卷积层和池化层，去除了所有全连接层。

GAN 基本原理以及数学证明

发表于 2020-08-14 更新于 2020-09-22 分类于深度学习 Disqus：
本文字数： 6.9k 阅读时长 ≈ 6 分钟
博客园同步已开启

Preface

今天在PD Lib和DL斗智斗勇时，突然想起了自己非常想学的GAN，机缘巧合下便百度了，得到了以下两篇文章：

于是便对GAN有了初步的了解（以前肯定是心不在焉才没有理解的（划掉）），随后又在五楼生命科学的书架上找到了相关资料，遂学了一波。

GAN概述

2014 年，Ian Goodfellow 和他在蒙特利尔大学的同事发表了一篇震撼学界的论文。没错，我说的就是《Generative Adversarial Nets》，这标志着生成对抗网络（GAN）的诞生，而这是通过对计算图和博弈论的创新性结合。他们的研究展示，给定充分的建模能力，两个博弈模型能够通过简单的反向传播（backpropagation）来协同训练。

这两个模型的角色定位十分鲜明。给定真实数据集 R，G 是生成器（generator），它的任务是生成能以假乱真的假数据；而 D 是判别器（discriminator），它从真实数据集或者 G 那里获取数据，然后做出判别真假的标记。Ian Goodfellow 的比喻是，G 就像一个赝品作坊，想要让做出来的东西尽可能接近真品，蒙混过关。而 D 就是文物鉴定专家，要能区分出真品和高仿（但在这个例子中，造假者 G 看不到原始数据，而只有 D 的鉴定结果——前者是在盲干）。

理想情况下，D 和 G 都会随着不断训练，做得越来越好——直到 G 基本上成为了一个“赝品制造大师”，而 D 因无法正确区分两种数据分布输给 G。

实践中，Ian Goodfellow 展示的这项技术在本质上是：G 能够对原始数据集进行一种无监督学习，找到以更低维度的方式（lower-dimensional manner）来表示数据的某种方法。而无监督学习之所以重要，就好像 Yann LeCun 的那句话：“无监督学习是蛋糕的糕体”。这句话中的蛋糕，指的是无数学者、开发者苦苦追寻的“真正的 AI”。
——pytorch实现GAN

GAN - Generative Adversarial Nets, 生成对抗网络，简单来讲其有两个组成部分：

D (Discriminator) - 判别器，判断输入时捏造的还是真实的
G (Generator) - 生成器，从随机噪声中生成我们想要的数据

随着训练的进行，我们要提高D的辨析能力，但同时也要G的能力来骗过D，因为我们的最终目的是要让G来生成可以骗过D的信息。总结来说，通过对这两个模型的训练，我们就可以找到随机噪声与有意义数据的映射，达到创作的目的。

GAN的流程和目标函数

GAN的目标函数

GAN的目标函数如下：

$V(D, G) = \mathbb E_{x \sim P_{\text{data}} } [\log D(x)] + \mathbb E_{\boldsymbol {z} \sim P_z}[\log(1 - D(G(\boldsymbol {z})))]$

其中，$D$为Discriminator的模型函数，$G$为Generator的模型函数，随机变量$x$服从原来正确的数据集的分布$P_\text {data}$，随机变量（这里可能是高维随机变量，取决于模型具体实现）$\boldsymbol {z}$服从分布$P_z$（生成噪音），$\mathbb E$代表期望。

GAN的流程

$G^* = \arg \min _G \max _D V(D, G)$

即，可以分为两步理解：

在$G$为常数的情况下，选择合适的$D$使得$V(D,G)$能够最大化。
在这之后，选取合适的$G$来最小化$V(D, G)$，这个$G$就是我们想要的生成模型。

在每一步的训练中：

取$m$个真实数据： $\{x^{(1)}, x^{(2)}, x^{(3)}, \cdots, x^{(m)}\}$ 使用$G$和$m$组随机数（服从于噪音分布$P_G$，一般使用服从正态分布的随机数） $\{\boldsymbol {z}^{(1)}, \boldsymbol {z}^{(2)}, \boldsymbol {z}^{(3)}, \cdots, \boldsymbol {z}^{(m)}\}$ 生成$m$个假数据，其中 $\forall i \in [1, m], i \in \mathbb Z \Rightarrow x^{(i)} \sim P_{\text{data}}, \boldsymbol {z} ^ {(i)} \sim P_z$
根据$\max$部分的目标使用随机梯度上升（Stochastic Gradient Ascent）更新$D$的参数，提高$D$的分辨能力 $\theta_d := \theta_d + \alpha_d \nabla_{\theta_d} \frac 1 m \sum _ {i = 1} ^ m \Big [ \log D\big ( x^{(i)} \big) + \log \big ( 1 - D \big ( G(\boldsymbol{z}^{(i)}) \big ) \big ) \Big]$
根据$\min$部分的目标使用随机梯度下降（Stochastic Gradient Descent）更新$G$的参数，使$G$生成的数据更有迷惑性 $\theta_g := \theta_g - \alpha_g\nabla_{\theta_g} \frac 1 m \sum _{i = 1} ^ m\log \Big ( 1 - D\big ( G(\boldsymbol{z} ^ {(i)})\big ) \Big )$

GAN的数学原理

Prerequisites

信息量(自信息)

信息量是指信息多少的量度，即，对于一条信息，传达这条信息所需的最少信息长度为自信息。

信息论创始人C.E.Shannon，1938年首次使用比特（bit）概念：1（bit）= $\log_2 2$。它相当于对二个可能结局所作的一次选择量。信息论采用对随机分布概率取对数的办法，解决了不定度的度量问题。

定义：符合分布$P$的某一事件$x$出现，传达出这条信息的信息量记为：

$I = \log \frac 1 {P(x)} = - \log P(x)$

香农熵

从离散分布$P$中随机抽选一个事件，传达这条信息所需的最优平均信息长度为香农熵，表达为：

$H(P) = \sum_x P(x) \log \frac 1 {P(x)} = - \sum_x P(x) \log P(x)$

若分布是连续的，则：

$H(P) = \int_x P(x) \log \frac 1 {P(x)} \mathrm dx = -\int_x P(x) \log P(x) \mathrm dx$

交叉熵

用分布$P$的最佳信息传递方式来传达分布$Q$中随机抽选的一个事件，所需的平均信息长度为交叉熵，表达为

$H_P(Q) = \sum_x Q(x) \log \frac 1 {P(x)} = - \sum_x Q(x) \log P(x)$ $H_P(Q) = \int_x Q(x) \log \frac 1 {P(x)} \mathrm dx = - \int_x Q(x) \log P(x) \mathrm dx$

$KL$ Divergence

$KL$散度：用分布$P$的最佳信息传递方式来传达分布$Q$，比用分布$Q$自己的最佳信息传递方式来传达分布$Q$，平均多耗费的信息长度为$KL$散度，表达为$D_P(Q)$或$D_{KL}(Q||P)$，$KL$散度衡量了两个分布之间的差异。

$\begin{aligned} D_{KL}(Q||P) = D_P(Q) &= H_P(Q) - H(Q) \\ &= \sum_x Q(x) \log \frac 1 {P(x)} - \sum _x Q(x) \log \frac 1 {Q(x)} \\ &= \sum_x Q(x) \log \frac {Q(x)} {P(x)} \end{aligned}$

对于连续分布：

$D_{KL}(Q||P) = D_P(Q) = \int_{-\infty} ^ {\infty} P(x)\log \frac {P(x)}{Q(x)} \mathrm dx$

KL Divergence越大，两个分布差异越大，反之差异越小。

数学原理

看完Prerequisites，我们回归正题讨论GAN的原理。我们现在想要做的事情，其实就是将一个服从$P_G$的随机噪声$\boldsymbol z$通过一个生成网络$G$得到一个和真实数据分布$P_{\text {data}}(x)$差不多的生成分布$P_G(x;\theta_g)$，其中$\theta_g$为生成网络$G$的参数。我们希望找到一个$\theta_g$使得两个分布$P_{\text {data}}(x)$与$P_G(x;\theta)$尽可能地相似（使得他们地KL散度尽可能得小）。

我们从真实数据分布$P_\text{data}(x)$中取$m$个样本，记作：

$\{x^{(1)}, x^{(2)}, x^{(3)}, \cdots, x^{(m)}\}$

根据生成网络的参数$\theta_g$，我们可以计算出这$m$个真实样本在生成网络中出现的概率$P_G(x^{(i)}; \theta_g)$，那么生成这样的$m$个样本数据的似然（likelihood）为：

$L = \prod_{i = 1} ^ m P_G(x^{(i)}; \theta_g)$

由于我们想要两个分布尽量相似，那么我们肯定希望这个似然$L$尽量大，即生成这样的真实数据的概率尽量大，遂我们最大化这个似然，找到$\theta_g^*$：

$\begin{aligned} \theta_g^* &= \arg \max _ {\theta_g} \prod _ {i = 1} ^ m P_G(x^{(i)}; \theta_g) \\ &\Leftrightarrow \arg \max _ {\theta_g} \log \prod _ {i = 1} ^ m P_G(x^{(i)}; \theta_g) \\ &= \arg \max _ {\theta_g} \sum_{i = 1} ^ m \log P_G(x^{(i)}; \theta_g) \\ &\approx \arg \max _ {\theta_g} \mathbb E_{x \sim P_{\text {data}}} [\log P_G(x; \theta_g)] \\ &= \arg \max _ {\theta_g} \int _ x P_\text{data}(x) \log P_G(x; \theta_g)\mathrm dx \\ &= \arg \max _ {\theta_g} \int _ x P_\text{data}(x) \log P_G(x; \theta_g)\mathrm dx \\&~~~~- \int _ x P_\text{data}(x) \log P_\text {data}(x)\mathrm dx \\ &= \arg \max _ {\theta_g} \int _ x P_\text {data} (x) \log \frac {P_G(x; \theta_g)} {P_\text {data}(x)} \mathrm dx \\ &= \arg \max _ {\theta_g} - \int _ x P_\text {data} (x) \log \frac {P_\text {data}(x)} {P_G(x; \theta_g)} \mathrm dx \\ &= \arg \min _ {\theta_g} KL(P_\text {data} || P_G(x; \theta)) \end{aligned}$

所以可见，其实最大化这个似然，和最小化KL散度是基本相同的。

上述式子中，$P_G(x;\theta_g)$代表在生成分布中出现$x$的概率，也可以如下计算得到：

$P_G(x) = \int _ \boldsymbol{z} P_z(z)\cdot 1\{G(z) = x\} \mathrm dz$

注：$1{\cdot}$的含义是若打括号内的逻辑运算为真则取$1$，假则取$0$. 即

$1\{\text {True}\} = 1, 1 \{\text {False}\} = 0$

但是我们发现，上述的过程是难以进行计算的，甚至完全没办法求$P_G(x)$，这只是模型的想法而已。

现在我们看回之前我们提到的目标函数：

$V(D, G) = \mathbb E_{x \sim P_{\text{data}} } [\log D(x)] + \mathbb E_{\boldsymbol {z} \sim P_z}[\log(1 - D(G(\boldsymbol {z})))]$

与最优化生成模型：

$G^* = \arg \min _G \max _D V(D, G)$

我们接下来分步解释。

首先，我们不妨解释一下$\max_D V(G, D)$，这部分的含义之前也解释过，是在给定$G$的情况下，最大化$V(G, D)$。观察发现，其形式其实与交叉熵损失函数非常相似：

$\mathcal L(\hat y, y) = -(y\log \hat y + (1 - y) \log (1 - \hat y))$

其实他们表达的目的也差不多。我们先化简一下$V(G, D)$看看能得到什么结果：

$\begin{aligned} V(G, D) &= \mathbb E_{x \sim P_{\text{data}} } [\log D(x)] + \mathbb E_{\boldsymbol {z} \sim P_z}[\log(1 - D(G(\boldsymbol {z})))] \\ &= \int_x P_\text {data}(x) \log D(x) \mathrm dx + \int_\boldsymbol{z} P_z(\boldsymbol{z}) \log (1 - D(G(\boldsymbol{z})))\mathrm dz \\ &= \int_x P_\text {data}(x) \log D(x) \mathrm dx + \int_x P_G(x)\log (1 - D(x)) \mathrm dx \\ &= \int_x [P_\text {data}(x) \log D(x) + P_G(x)\log (1 - D(x))] \mathrm dx \end{aligned}$

让我们考察积分内部的项，我们可以对它做指数运算，即：

$e^{P_\text {data}(x) \log D(x) + P_G(x)\log (1 - D(x))} = D(x) ^ {P_\text {data}}\times(1- D(x))^{P_G(x)}$

其想表达什么便不言而喻了，它表达的就是判别器判别是真的的正确率和判别是假的的正确率，总体来说就是衡量$D$的能力，所以我们想要最大化$V$，提高$D$的判别能力。

令

$f(D) = P_\text {data}(x) \log D(x) \mathrm dx + P_G(x)\log (1 - D(x))$

因为这里$P_\text {data} (x)$和$P_G(x)$都可以看作常数，所以

$\arg \max _ D \int_x f(D) \mathrm dx = \arg \max _D f(D)$

最大化$f(D)$，即令其导数为$0$：

$\frac {\mathrm d f(D)} {\mathrm dD } = \frac {P_\text {data}(x)}{D} - \frac {P_G(x)} {1 - D} = 0$

则：

$\frac {P_\text {data}(x)}{D} = \frac {P_G(x)} {1 - D}$ $D^*(x) = \frac {P_\text {data}(x)}{P_\text {data}(x) + P_G(x)}$

这样，我们就得到了那个状态下最优的$D^*$的表达式。我们将这个能够最大化$V$的$D$代入回$V(G, D)$：

$\begin{aligned} \max V(G, D) &= V(G, D^*) \\ &= \mathbb E_{x \sim P_\text {data}} \Big [ \log \frac {P_\text {data}(x)}{P_\text {data}(x) + P_G(x)} \Big] + \mathbb E_{x \sim P_G} \Big [ \frac {P_G(x)}{P_\text {data}(x) + P_G(x)}\Big ] \\ &= \int_x P_\text {data} (x) \log \frac {\frac 1 2 P_\text {data}}{\frac 1 2 (P_\text{data}(x) + P_G(x))} \mathrm dx + \int _ x P_G(x) \log \frac {\frac 1 2 P_G(x)} {\frac 1 2 (P_\text {data} (x) + P_G(x))} \mathrm dx \\ &= -2\log 2 + D_{KL} (P_\text {data} || \frac 1 2 [P_\text{data}(x) + P_G(x)]) + D_{KL} (P_G(x) || \frac 1 2 [P_\text {data}(x) + P_G(x)]) \\ &= -2\log 2 + JSD (P_\text{data}(x) || P_G(x)) \end{aligned}$

其中，我们引入了$JS$ Divergence，定义如下：

$JSD(P||Q) = \frac 1 2 D_{KL} (P||M) + \frac 1 2 D_{KL} (Q || M), M = \frac 1 2 (P + Q)$

容易得到，KL Divergence是不对称的，而JS Divergence是对称的。他们都可以衡量两组分布建的差异。这里我们想要两组分布差异最小，故取$\min$

所以，这也就解释了为什么：

$\arg \min _G \max _D V(G, D)$

是我们的目标过程。