gyro永不抽风

ああああああああああああああああおおおおおおおおおおおおおおおお

发表于 更新于 分类于 Disqus：
本文字数： 119 阅读时长 ≈ 1 分钟

感谢这个博客，

感谢没有冒号的拍拍二次元人们，

一起撑过了2020这艰难的一年的大部分时间。

2020-03 ~ 2020-11

奶茶铺结束营业咯（（

新店就开在隔壁：gyrojeff.top

老的烦心事就不再迁移了

过段时间把技术文章慢慢迁…咕咕咕///

发表于 分类于 Disqus：
本文字数： 1.1k 阅读时长 ≈ 1 分钟
博客园 同步已开启

使用Docker直接部署MySQL

拉取官方最新的MySQL镜像：

1
docker pull mysql:latest

运行：

1
docker run --name <name> -e MY_ROOT_PASSWORD=<root_password> -p <port>:3306 -d mysql:<tag>

其中：

  • <name>填入容器的命名
  • <root_password>填入数据库root用户的密码
  • <port>填入想要对外映射的端口
  • <tag>是镜像的版本号，建议填latest

传送门：https://hub.docker.com/r/library/mysql/

Docker的一些常用命令

查看所有Docker:

1
sudo docker ps -a

删除一个容器：

1
sudo docker rm <name>

停止：

1
sudo docker stop <name>

暂停：

1
sudo docker pause <name>

重启：

1
sudo docker restart <name>

让容器执行命令：

1
sudo docker exec -it <name> <exec>

其中：

  • <name>是容器名称
  • <exec>是命令

  • -it的官方解释：

    1
    2
    3
    4
    5
    6
    7
    8
    -d, --detach               Detached mode: run command in the background
        --detach-keys string   Override the key sequence for detaching a container
    -e, --env list             Set environment variables
    -i, --interactive          Keep STDIN open even if not attached
        --privileged           Give extended privileges to the command
    -t, --tty                  Allocate a pseudo-TTY
    -u, --user string          Username or UID (format: <name|uid>[:<group|gid>])
    -w, --workdir string       Working directory inside the container

    所以进入容器其实可以直接 (如果对方有/bin/bash)：

    1
    docker exec -it <name> /bin/bash

其余的请直接查看help:

1
sudo docker --help
1
sudo docker <exec> --help

发表于 更新于 分类于 Disqus：
本文字数： 947 阅读时长 ≈ 1 分钟
博客园 同步已开启

安装Docker

卸载旧版本

1
sudo apt-get remove docker docker-engine docker.io containerd runc

设置仓库

安装apt依赖包：

1
2
3
4
5
6
sudo apt-get install \
    apt-transport-https \
    ca-certificates \
    curl \
    gnupg-agent \
    software-properties-common

添加官方GPG密钥：

1
curl -fsSL https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu/gpg | sudo apt-key add -

9DC8 5822 9FC7 DD38 854A E2D8 8D81 803C 0EBF CD88 通过搜索指纹的后8个字符，验证您现在是否拥有带有指纹的密钥。

1
2
3
4
5
6
$ sudo apt-key fingerprint 0EBFCD88
   
pub   rsa4096 2017-02-22 [SCEA]
      9DC8 5822 9FC7 DD38 854A  E2D8 8D81 803C 0EBF CD88
uid           [ unknown] Docker Release (CE deb) <[email protected]>
sub   rsa4096 2017-02-22 [S]

使用以下指令设置稳定版仓库

1
2
3
4
sudo add-apt-repository \
   "deb [arch=amd64] https://mirrors.ustc.edu.cn/docker-ce/linux/ubuntu/ \
  $(lsb_release -cs) \
  stable"

安装 Docker Engine-Community

更新 apt 包索引。

1
sudo apt-get update

安装最新版本的 Docker Engine-Community 和 containerd:

1
sudo apt-get install docker-ce docker-ce-cli containerd.io

Docker换源

  1. 先进入阿里云开发社区,并找到控制台：https://developer.aliyun.com/
  2. 搜索容器镜像服务：
  3. 按照图片当中的做：

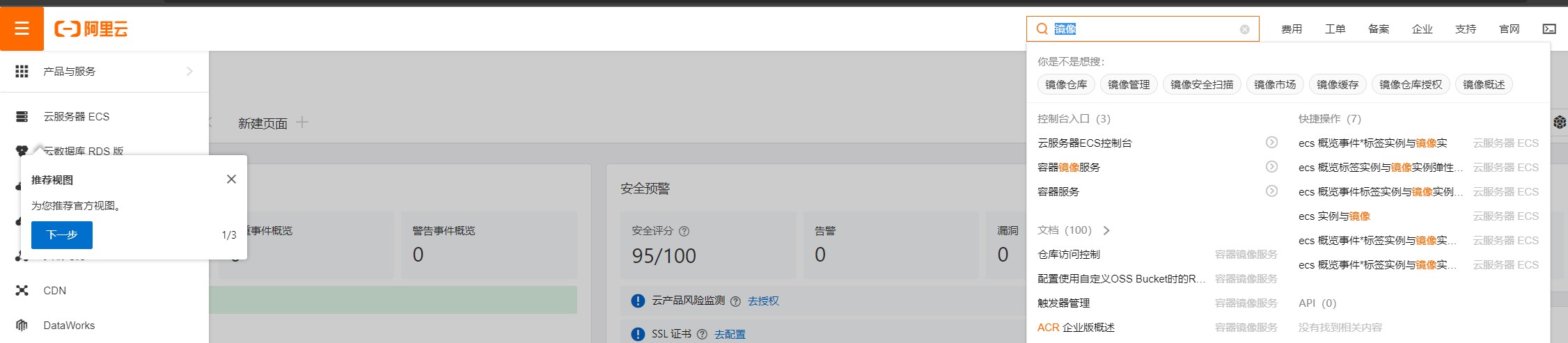
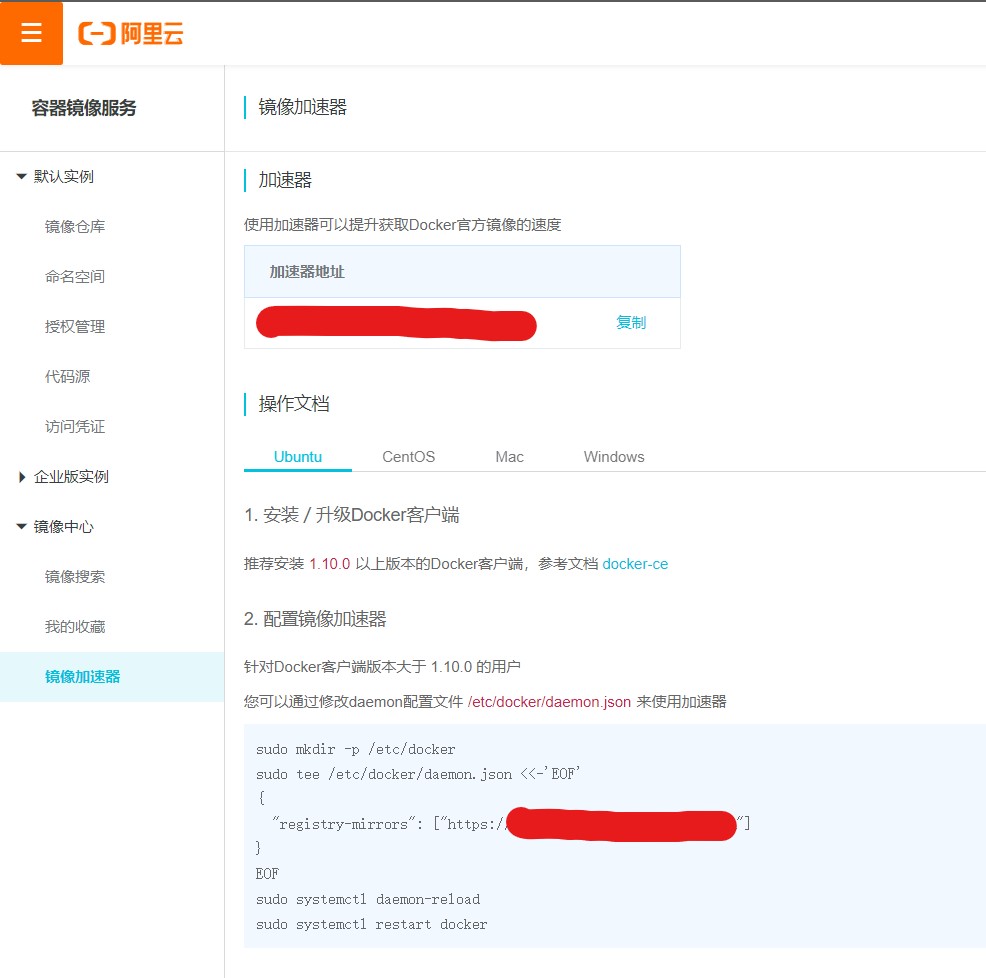
确认成功的方法：

1
sudo docker info

观察最后几行当中Registry Mirrors有没有出现。

发表于 更新于 分类于 Disqus：
本文字数： 3.5k 阅读时长 ≈ 3 分钟
博客园 同步已开启

购买

趁着双十一，租了腾讯云3年的VPS，这个价钱是真的够便宜的了（确信）。

安装系统

我选择的是Ubuntu 18.04 LTS，腾讯云的控制台当中可以选择重装。

提醒：由于我当时不停得重装系统（自己菜），所以ssh有的时候连接会出现问题：

“IT’S POSSIBLE THAT SOMEONE IS DOING SOMETHING NASTY!!!”

确实，NASTY是我本人了。这个时候你只需要在你的本地执行：

1
sudo rm ~/.ssh/known_hosts

这样可以删除你的所有连接信息，不会报错。

换源

首先ssh连接VPS，然后进行super cow power的apt换源（大雾），其中我用的是阿里云的源

人是腾讯人，心是阿里心
（大雾）

1
2
sudo rm /etc/apt/sources.list
sudo vim /etc/apt/sources.list
1
2
3
4
5
6
7
8
9
10
11
# 阿里源
deb http://mirrors.aliyun.com/ubuntu/ bionic main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ bionic-security main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ bionic-updates main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ bionic-proposed main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ bionic-backports main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ bionic main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ bionic-security main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ bionic-updates main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ bionic-proposed main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ bionic-backports main restricted universe multiverse

更新：

1
sudo apt update && sudo apt upgrade

其中可能会碰到如下情况：

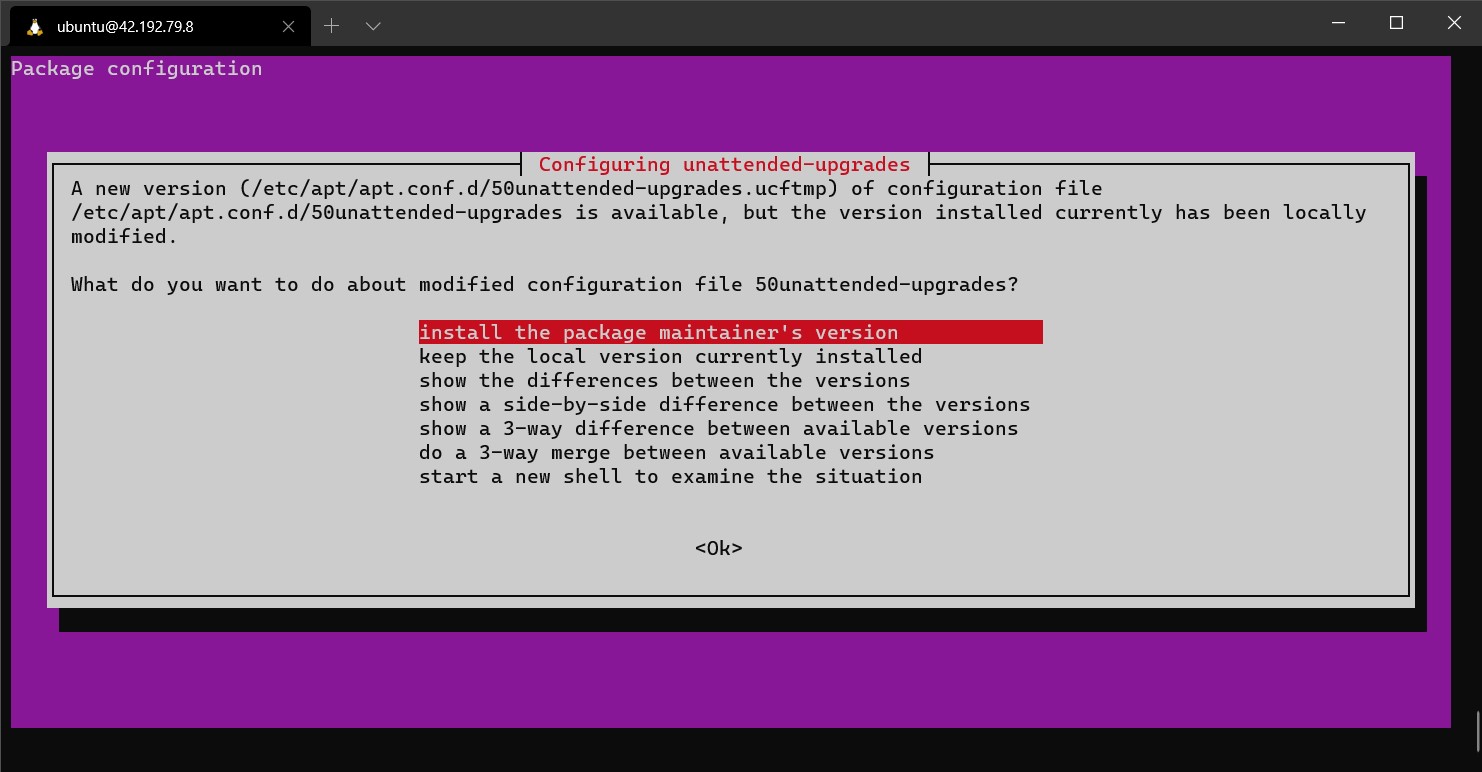
选择第一个安装新版。

搭建LAMP

LAMP: Linux, Apache, MySQL, PHP

安装Apache2:

1
sudo apt install apache2

安装PHP:

1
sudo apt install php php-dev php-curl php-pear php-mysql libapache2-mod-php php-mbstring

部署Typecho

官网：http://typecho.org/download

不管通过什么东西，让下载下来，解压好，build目录中的所有文件，出现在/var/www当中

  • 鄙人由于不精通命令行，所以本机下载然后解压然后通过sftp的方式传过去
  • 方法很多，不用拘泥

配置Apache2服务器

根据前面的保存的路径修改配置文件：

1
sudo vim /etc/apache2/sites-available/000-default.conf

修改：

1
2
3
4
<VirtualHost *:80>
...
        ServerAdmin webmaster@localhost
        DocumentRoot /var/www		# 原来：/var/www/html

安装MySQL

由于安装过程中不一定要求输入密码，所以可能已经生成好了默认密码。打开：

1
sudo vim /etc/mysql/debian.cnf

这里面有用户名和密码，用debian-sys-maint登录MySQL: 

1
mysql -u debian-sys-maint -p

修改root账号密码：

1
update mysql.user set authentication_string=password('<your_pwd>') where user='root' and Host ='localhost';

防止登录密码失效：

1
2
use mysql;
update user set plugin="mysql_native_password";

刷新，退出：

1
2
flush privileges;
quit;

重启服务：

1
sudo service mysql restart

Navicat登录MySQL

目前我只有在SSH的情况下成功登录了MySQL，原因不明。

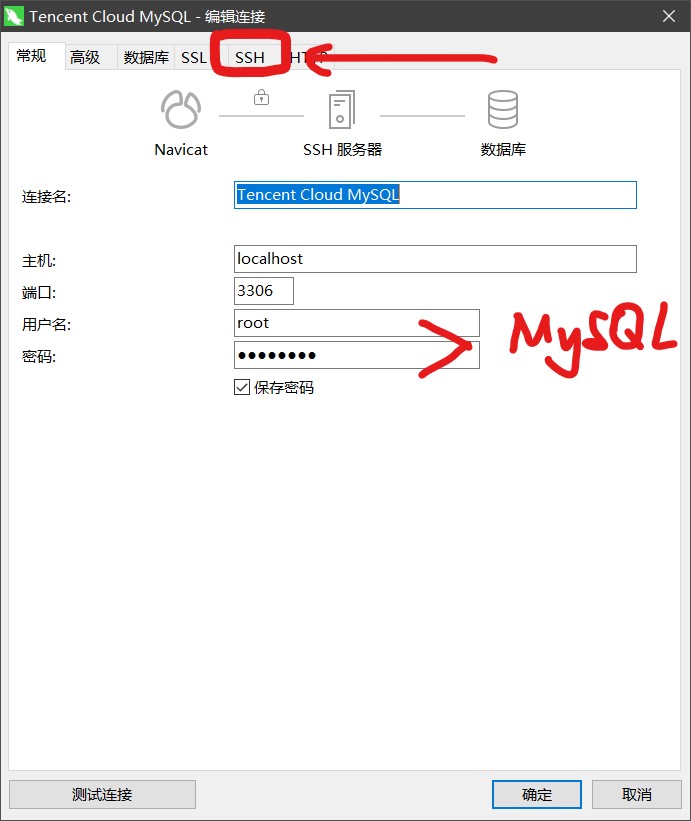
然后选到mysql，找到user，接下来那个原始账号想删就能删了。

部署SSL

由于我也购买了腾讯云的域名（第一年只要4块！！！往后只要25块！！！）所以可以直接在腾讯云申请SSL。

腾讯免费ssl证书获取链接：https://console.cloud.tencent.com/ssl

按照要求填写，然后第二步认证直接采用推荐方式，这样就可以直接配置好NameServer，不用自己操心。等到审核成功之后：

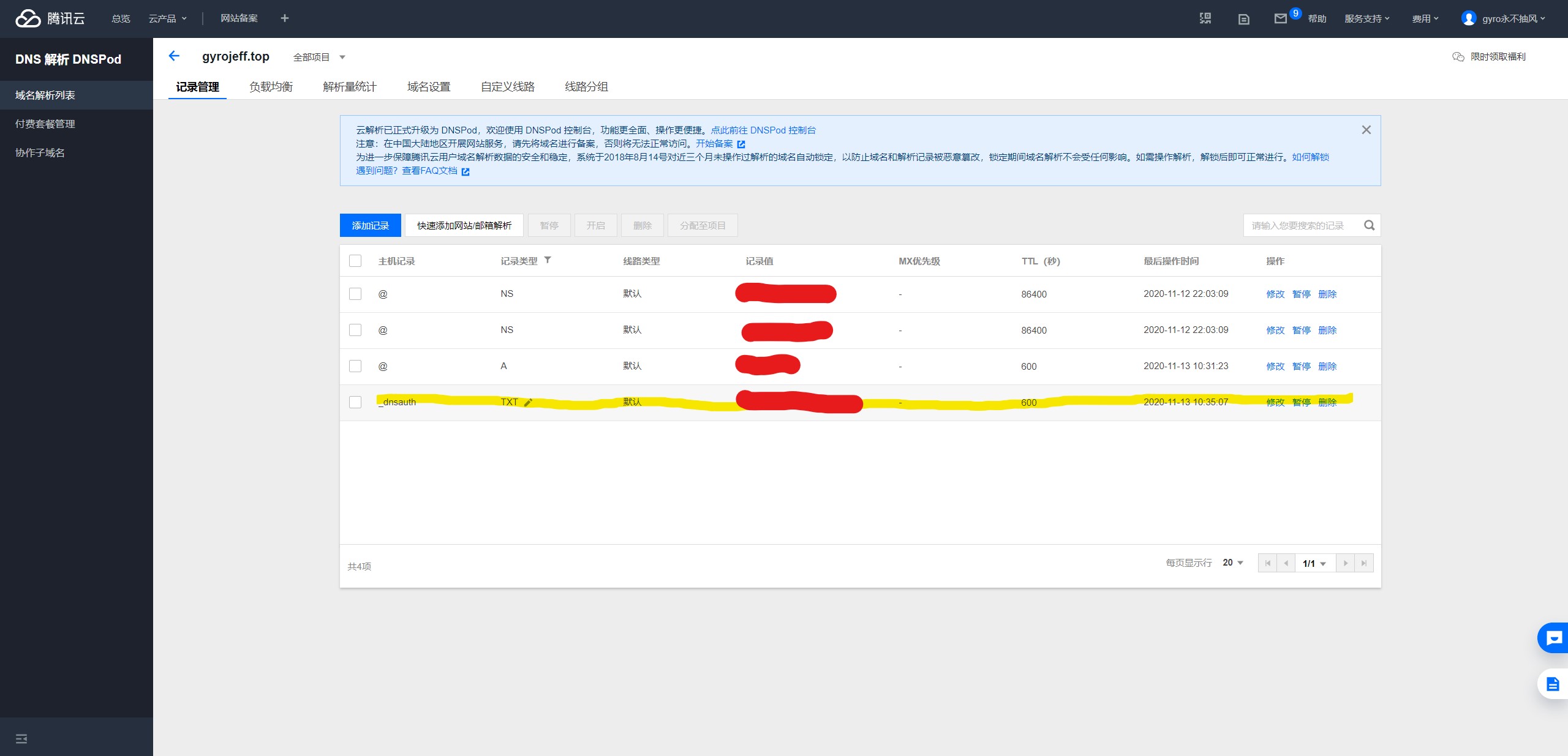
会自动出现TXT记录。

接下来，我们将审核通过的证书加载下来（右侧有下载按钮）：

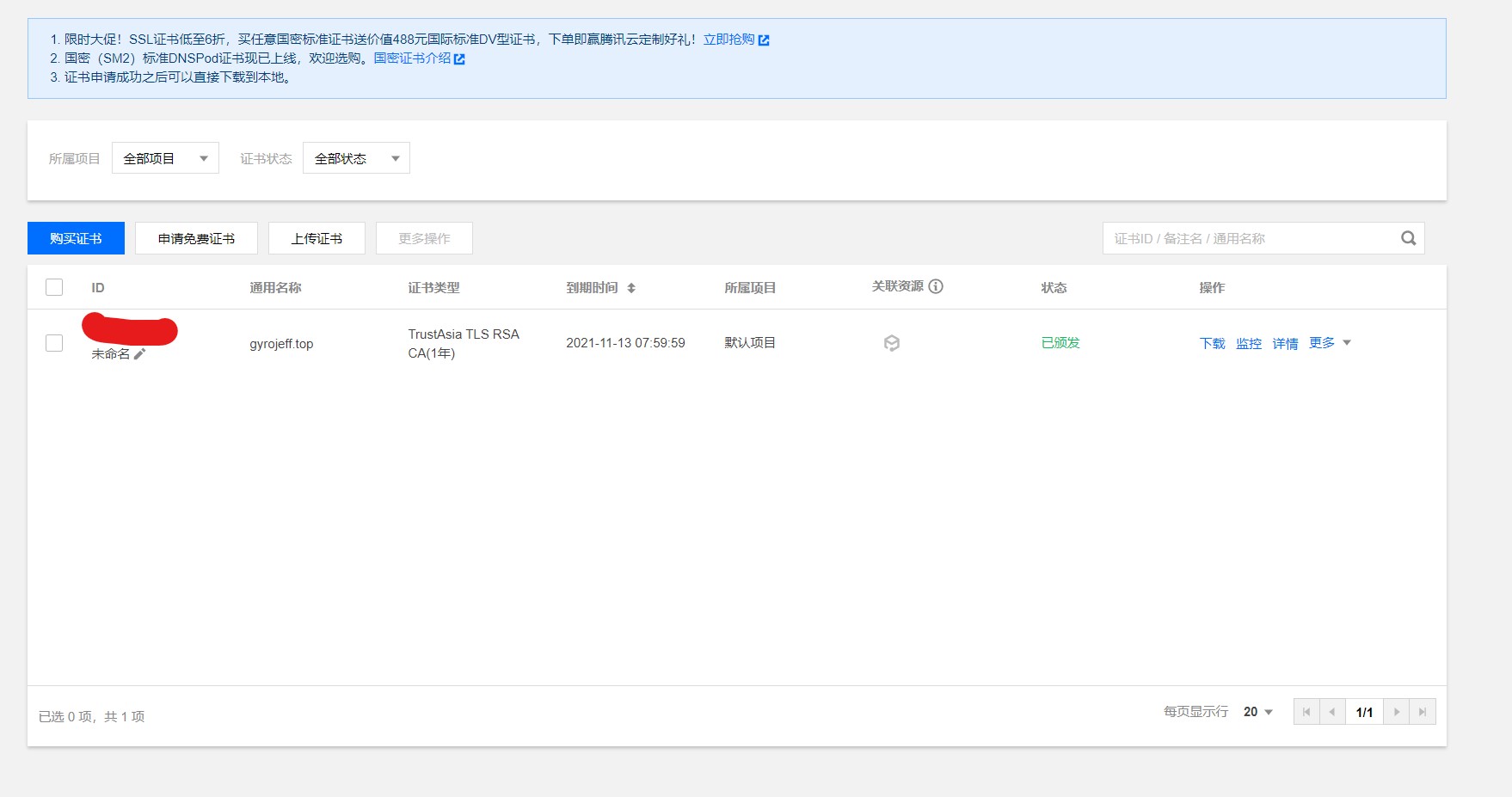
解压之后会有以下几种类型web服务器的证书，选择Apache，可以看到里面包含三个文件：

将它们上传到VPS的/etc/httpd/ssl目录（其实并非非他不可，但我懒了）。

然后，开启ssl模块：

1
sudo a2enmod ssl

查看/etc/apache2/ports.conf文件中，是不是包含（没有的话，添加）

1
2
Listen 80
Listen 443

接着我们需要创建软连接，同时删除/etc/apache2/sites-enabled/site-enabled目录下的000-default.conf链接文件

1
2
sudo ln -s /etc/apache2/sites-available/default-ssl.conf /etc/apache2/sites-enabled/default-ssl.conf
sudo rm /etc/apache2/sites-enabled/000-default.conf

接着配置default-ssl.conf这个文件

1
sudo vim /etc/apache2/sites-enabled/default-ssl.conf

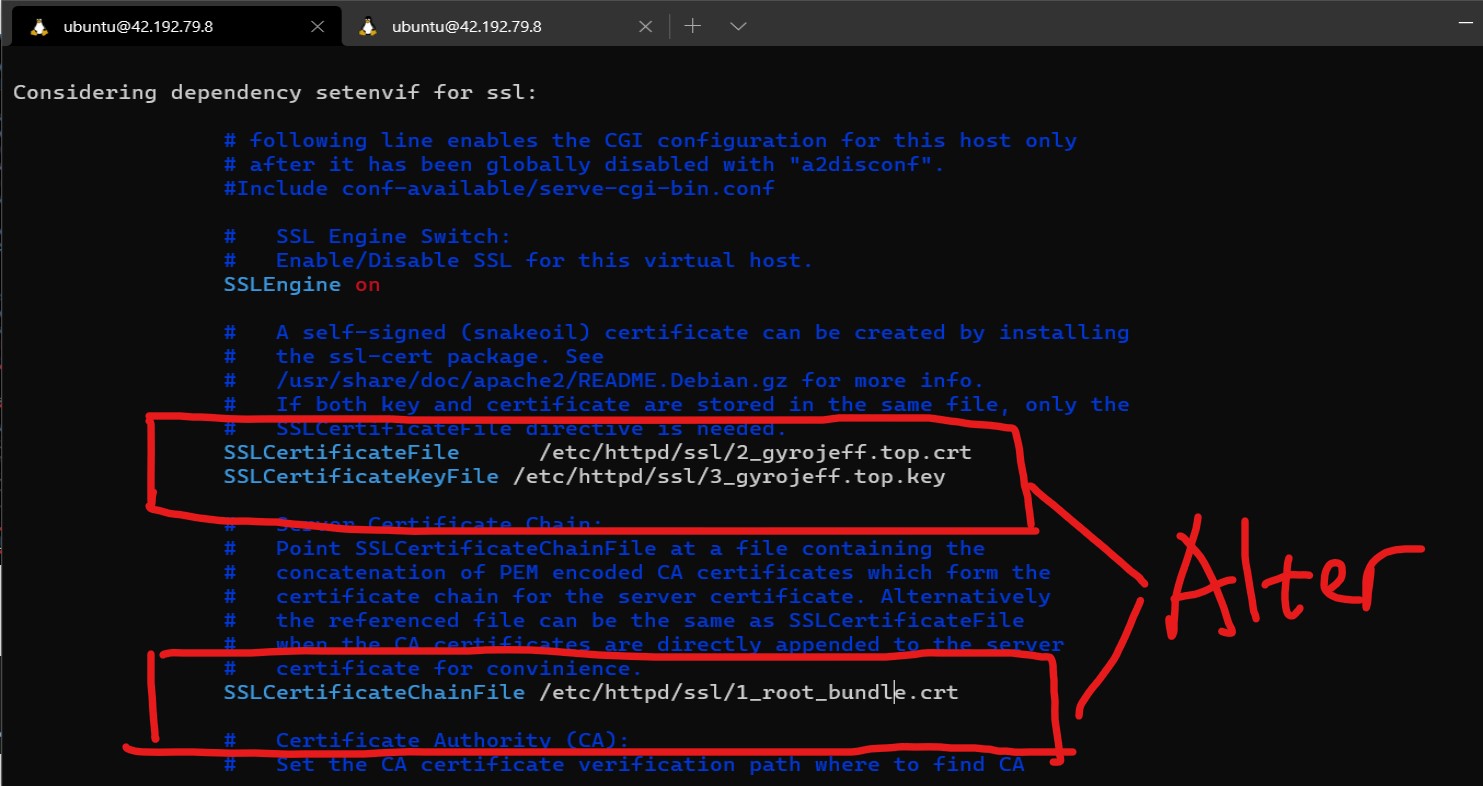
（懂我意思就好）（小声）

接着我们配置http重定向为https

开启rewrite模块：

1
sudo a2enmod rewrite

接着配置/etc/apache2/apache2.conf文件，在文件的末尾添加:

1
2
3
4
5
6
<Directory "/var/www">
  # 新增
  RewriteEngine on
  RewriteCond %{SERVER_PORT} !^443$
  RewriteRule ^(.*)?$ https://%{SERVER_NAME}%{REQUEST_URI} [L,R]
</Directory>

这样就可以让http自动跳转到https。

最后重启Apache2服务：

1
sudo service apache2 restart

安装Typecho

进入博客所在网址，开始安装。填写：

  • 选择MySQL
  • 数据库地址：localhost
  • 端口（若更改过请填写更改后的端口），3306
  • 数据库用户名：root
  • 数据库密码：设置的密码
  • 域名
  • 管理员账号
  • 管理员密码
  • …

接下来按照网页指示操作即可，注：网站根目录是/var/www

发表于 分类于 Disqus：
本文字数： 244 阅读时长 ≈ 1 分钟

人到底为什么要活着呢？

总感觉，现在活着只是为了活着。

考试到底什么时候才有尽头呢？

到底什么时候才能获得解脱呢？

到底是从什么时候开始爸妈习以为常地觉得我优秀呢？

明明是承认自己的不足但为什么永远会被认为是装逼呢？

努力到底有什么用呢？

到头来还是一无是处。

一件事做得有瑕疵变成了一辈子叨念的话题。

一件事做得不对变成为了一生的污点。

我为什么没有资格选择想不想来到这个世界呢？

为什么要惩罚我让我出生呢？

为什么为了活下去就要回应别人的期待呢？

为什么从出生一开始便是欠别人的呢？

为什么会这么空虚痛苦无力呢？

发表于 分类于 Disqus：
本文字数： 2.2k 阅读时长 ≈ 2 分钟
博客园 同步已开启

题目

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 nn 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

主件 附件
电脑 打印机，扫描仪
书柜 图书
书桌 台灯，文具
工作椅 无

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有 00 个、11 个或 22 个附件。每个附件对应一个主件，附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 nn 元。于是，他把每件物品规定了一个重要度，分为 55 等：用整数 1∼51 \sim 5 表示，第 55 等最重要。他还从因特网上查到了每件物品的价格（都是 1010 元的整数倍）。他希望在不超过 nn 元的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 jj 件物品的价格为 vjv_j，重要度为wjw_j，共选中了 kk 件物品，编号依次为 j1,j2,…,jkj_1,j_2,\dots,j_k，则所求的总和为：

vj1×wj1+vj2×wj2+⋯+vjk×wjkv_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}。

请你帮助金明设计一个满足要求的购物单。

输入格式

第一行有两个整数，分别表示总钱数 nn 和希望购买的物品个数 mm。

第 22 到第 (m+1)(m + 1) 行，每行三个整数，第 (i+1)(i + 1) 行的整数 viv_i，pip_i，qiq_i 分别表示第 ii 件物品的价格、重要度以及它对应的的主件。如果 qi=0q_i=0，表示该物品本身是主件。

输出格式

输出一行一个整数表示答案。

输入输出样例

输入 #1 
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出 #1 
2200

说明/提示

数据规模与约定

对于全部的测试点，保证 1≤n≤3.2×1041 \leq n \leq 3.2 \times 10^4，1≤m≤601 \leq m \leq 60，0≤vi≤1040 \leq v_i \leq 10^4，1≤pi≤51 \leq p_i \leq 5，0≤qi≤m0 \leq q_i \leq m，答案不超过 2×1052 \times 10^5。

题解

这道题可以只枚举主要物品，有五种选择方法：

  • 主
  • 主 + 副1
  • 主 + 副2
  • 主 + 副1 + 副2
  • 不选

然后其实就是普通的背包问题了（撒花

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>

using namespace std;

const int maxm = 65;
const int maxn = 32005;

int pos[maxm], cnt[maxm], f[maxn];
struct node { int v, p; } a[maxm][3];

int main() {
	int n, m, k = 0;
	cin >> n >> m;
	for (int i = 1; i <= m; i ++) {
		int v, p, q; cin >> v >> p >> q;
		if (q == 0) {
			a[++ k][0] = (node) { v, p };
			pos[i] = k;
		} else a[pos[q]][++ cnt[q]] = (node) { v, p };
	}
	for (int i = 1; i <= k; i ++) {
		for (int j = n; j >= a[i][0].v; j --) {
			if (j >= a[i][0].v + a[i][1].v + a[i][2].v)
				f[j] = max(f[j], f[j - (a[i][0].v + a[i][1].v + a[i][2].v)] + a[i][0].v * a[i][0].p + a[i][1].v * a[i][1].p + a[i][2].v * a[i][2].p);
			if (j >= a[i][0].v + a[i][1].v)
				f[j] = max(f[j], f[j - (a[i][0].v + a[i][1].v)] + a[i][0].v * a[i][0].p + a[i][1].v * a[i][1].p);
			if (j >= a[i][0].v + a[i][2].v)
				f[j] = max(f[j], f[j - (a[i][0].v + a[i][2].v)] + a[i][0].v * a[i][0].p + a[i][2].v * a[i][2].p);
			if (j >= a[i][0].v)
				f[j] = max(f[j], f[j - a[i][0].v] + a[i][0].v * a[i][0].p);
		}
	}
	cout << f[n] << endl;
	return 0;
}

发表于 分类于 Disqus：
本文字数： 3.9k 阅读时长 ≈ 4 分钟
博客园 同步已开启

题目

题目描述

设 T=(V,E,W)T=(V,E,W) 是一个无圈且连通的无向图（也称为无根树），每条边到有正整数的权，我们称 TT 为树网（treenetwork），其中 VV，EE 分别表示结点与边的集合，WW 表示各边长度的集合，并设 TT 有 nn 个结点。

路径：树网中任何两结点 aa，bb 都存在唯一的一条简单路径，用 d(a,b)d(a, b) 表示以 a,ba, b 为端点的路径的长度，它是该路径上各边长度之和。我们称 d(a,b)d(a, b) 为 a,ba, b 两结点间的距离。

D(v,P)=min⁡{d(v,u)}D(v, P)=\min\{d(v, u)\}, uu 为路径 PP 上的结点。

树网的直径：树网中最长的路径成为树网的直径。对于给定的树网 TT，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距 ECC(F)\mathrm{ECC}(F)：树网 TT 中距路径 FF 最远的结点到路径 FF 的距离，即

ECC(F)=max⁡{d(v,F),v∈V}\mathrm{ECC}(F)=\max\{d(v, F),v \in V\}

任务：对于给定的树网 T=(V,E,W)T=(V, E, W) 和非负整数 ss，求一个路径 FF，他是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过 ss（可以等于 ss），使偏心距 ECC(F)ECC(F) 最小。我们称这个路径为树网 T=(V,E,W)T=(V, E, W) 的核（Core）。必要时，FF 可以退化为某个结点。一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

下面的图给出了树网的一个实例。图中，A−BA-B 与 A−CA-C 是两条直径，长度均为 2020。点 WW 是树网的中心，EFEF 边的长度为 55。如果指定 s=11s=11，则树网的核为路径DEFG（也可以取为路径DEF），偏心距为 88。如果指定 s=0s=0（或 s=1s=1、s=2s=2），则树网的核为结点 FF，偏心距为 1212。

输入格式

共 nn 行。

第 11 行，两个正整数 nn 和 ss，中间用一个空格隔开。其中 nn 为树网结点的个数，ss 为树网的核的长度的上界。设结点编号以此为 1,2…,n1,2\dots,n。

从第 22 行到第 nn 行，每行给出 33 个用空格隔开的正整数 u,v,wu, v, w，依次表示每一条边的两个端点编号和长度。例如，2 4 7 表示连接结点 22 与 44 的边的长度为 77。

输出格式

一个非负整数，为指定意义下的最小偏心距。

输入输出样例

输入 #1 
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出 #1 
5
输入 #2 
8 6
1 3 2
2 3 2 
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3
输出 #2 
5

说明/提示

  • 对于 40%40\% 的数据，保证 n≤15n \le 15。
  • 对于 70%70\% 的数据，保证 n≤80n \le 80。
  • 对于 100%100\% 的数据，保证 n≤300n \le 300，0≤s≤1030\le s\le10^3，1≤u,v≤n1 \leq u, v \leq n，1≤w≤1031 \leq w \leq 10^3。

题解

因为路径$F$是直径上的一部分，那就变得非常好办了。考虑下图的样子：

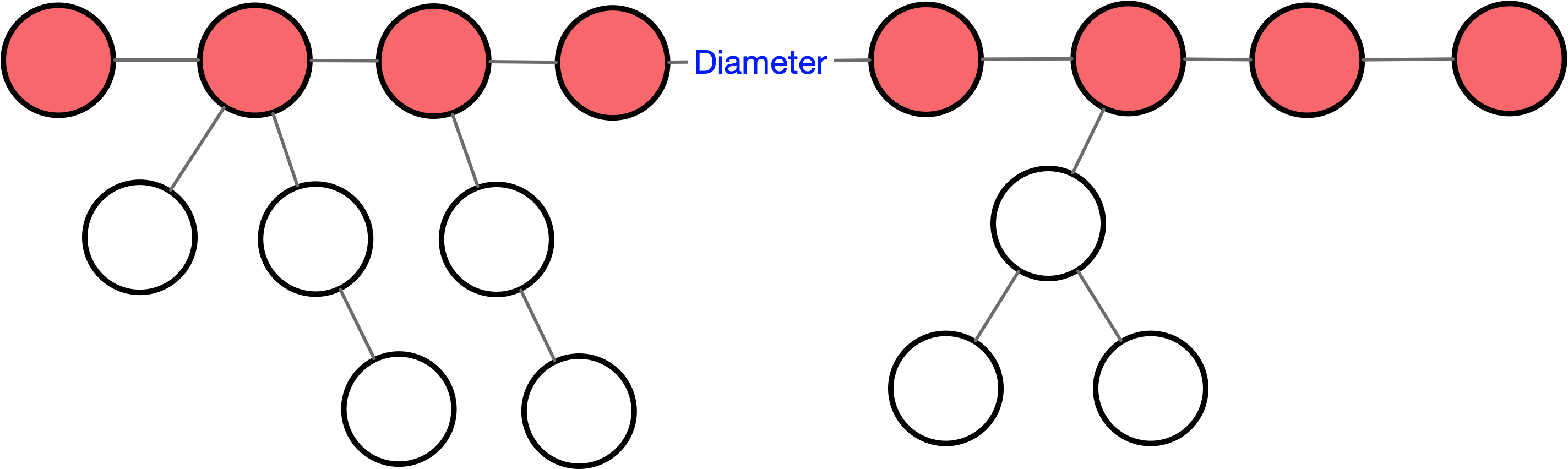
求出在这种情况之下的子树的最深深度，记为$sd\text{ }secd[i]$，其中$i$为直径上的点，之所以这么表示，因为这个深度是在一个节点所有子树当中第二深的深度，最深的深度$sd\text{ }max[i]$为直径所在的那颗子树的深度。

在这种情况下，可以在直径上选定一段$F$后，列出$ECC(F)$的方程：

因为求上面是式子中的第一项和第三项非常容易，在直径求完之后就是$O(1)$了，而第二项是区间最大值，那么我们可以用单调队列维护。

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <iostream>
#include <cstring>
#define int long long 

using namespace std;

const int maxn = 305;
int h[maxn], ecnt = 2, n, s;
struct edge { int to, next, w; } g[maxn << 1];
void add_edge(int u, int v, int w) { g[ecnt] = (edge) { v, h[u], w }; h[u] = ecnt ++; }
struct node { int pos, val; } q[maxn];

// sd_max: maximum depth of subtree
// sd_secd: second maximum depth of subtree
int dis[maxn], sd_max[maxn], sd_secd[maxn], next[maxn], dia[maxn], head, tail; 
	
int dfs1(int u, int fa) {
	int alpha = u;
	for (int e = h[u]; e; e = g[e].next) {
		int v = g[e].to;
		if (v == fa) continue;
		dis[v] = dis[u] + g[e].w;
		int a = dfs1(v, u);
		if (dis[a] >= dis[alpha]) alpha = a;
	}
	return alpha;
}

void dfs2(int u, int fa) {
	for (int e = h[u]; e; e = g[e].next) {
		int v = g[e].to;
		if (v == fa) continue;
		dis[v] = dis[u] + g[e].w;
		dfs2(v, u);
		int this_depth = sd_max[v] + g[e].w;
		if (this_depth >= sd_max[u]) {
			sd_secd[u] = sd_max[u];
			sd_max[u] = this_depth;
			next[u] = v;
		} else if (this_depth > sd_secd[u]) {
			sd_secd[u] = this_depth;
		}
	}
}

void inc(long long &i) {
	i ++;
	while (head < tail && q[head].pos == i - 1) head ++;
}

signed main() {
	cin >> n >> s;
	for (int i = 1; i < n; i ++) {
		int u, v, w; cin >> u >> v >> w;
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
	int ds = dfs1(1, 0);
	dis[ds] = 0;
	dfs2(ds, 0);
	int k = 0;
	for (int p = ds; p; p = next[p])
		dia[++ k] = p;
		
		
//	for (int i = 1; i <= k; i ++) cout << dia[i] << endl;
//	for (int i = 1; i <= k; i ++) cout << sd_secd[dia[i]] << endl; 
//	for (int i = 1; i <= k; i ++) cout << dis[dia[i]] << endl; 
	
	
	int ans = 8e18;
	head = 0, tail = 0;
	for (int i = 1, j = 1; i <= k; inc(i)) {
		int u = dia[i];
		while (j + 1 <= k + 1 && dis[dia[j]] - dis[u] <= s) {
			while (head < tail && q[tail - 1].val <= sd_secd[dia[j]]) tail --;
			q[tail ++] = (node) { j, sd_secd[dia[j]] };
			j ++;
		}
		int tmp = max(dis[u], dis[dia[k]] - dis[dia[j - 1]]);
		tmp = max(tmp, q[head].val);
		ans = min(ans, tmp);
	}
	cout << ans << endl;
	return 0;
}

发表于 分类于 Disqus：
本文字数： 2.6k 阅读时长 ≈ 2 分钟
博客园 同步已开启

题目

Computer

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 43138    Accepted Submission(s): 8426


Problem Description
A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.


Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.
 

Input
Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.
 

Output
For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).
 

Sample Input
5
1 1
2 1
3 1
1 1
 

Sample Output
3
2
3
4
4
 

Author
scnu

题解

我们要求每一个端点最远点，其实就是这个端点到任意一条直径两个端点距离较远的那一个。证明过程其实非常的简单，用反证法就可以。那么，我们其实只需要用两遍dfs求一下直径的两个端点和到一个端点的距离数组求出来，再用一遍dfs把到另外一个端点的距离数组求出来。

注意

多组数据，用while (scanf("%d", &n) != EOF)来做。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

const int maxn = 10005;

int head[maxn], ecnt = 2, dis[maxn], dis2[maxn];
struct edge { int to, next, w; } g[maxn << 1];
void add_edge(int u, int v, int w) { g[ecnt] = (edge) { v, head[u], w }; head[u] = ecnt ++; } 

int n;

int dfs1(int u, int fa) {
	int alpha = u;
	for (int e = head[u]; e; e = g[e].next) {
		int v = g[e].to;
		if (v == fa) continue;
		dis[v] = dis[u] + g[e].w;
		int a = dfs1(v, u);
		if (dis[a] >= dis[alpha]) alpha = a;
	}
	return alpha;
}

int dfs2(int u, int fa) {
	for (int e = head[u]; e; e = g[e].next) {
		int v = g[e].to;
		if (v == fa) continue;
		dis2[v] = dis2[u] + g[e].w;
		dfs2(v, u);
	}
}

int main() {
	while (scanf("%d", &n) != EOF) {
		memset(head, 0, sizeof(head));
		memset(g, 0, sizeof(g));
		ecnt = 2;
		for (int i = 2; i <= n; i ++) {
			int v, w; cin >> v >> w;
			add_edge(i, v, w); add_edge(v, i, w);
		}
		int ds = dfs1(1, 0);
		int tmp = dis[ds];
		dis[ds] = 0;
		int dt = dfs1(ds, 0);
		dis2[dt] = 0;
		dfs2(dt, 0);
		for (int i = 1; i <= n; i ++) cout << max(dis[i], dis2[i]) << endl;
	}
	return 0;
}

发表于 分类于 Disqus：
本文字数： 2.2k 阅读时长 ≈ 2 分钟
博客园 同步已开启

题目

题目描述

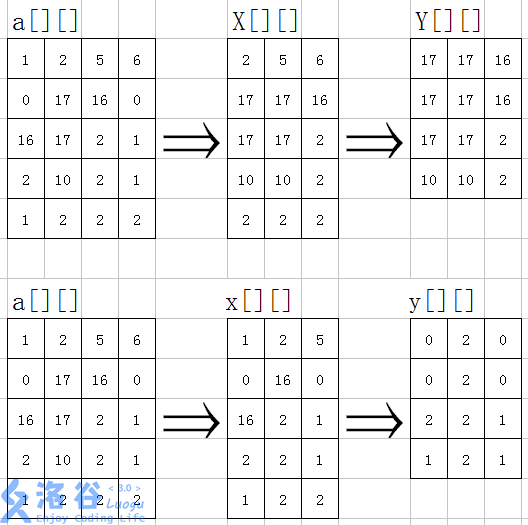
有一个a*b的整数组成的矩阵，现请你从中找出一个n*n的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为3个整数，分别表示a,b,n的值

第二行至第a+1行每行为b个非负整数，表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。

输出格式

仅一个整数，为a*b矩阵中所有“n*n正方形区域中的最大整数和最小整数的差值”的最小值。

输入输出样例

输入 #1 
5 4 2
1 2 5 6
0 17 16 0
16 17 2 1
2 10 2 1
1 2 2 2
输出 #1 
1

说明/提示

问题规模

（1）矩阵中的所有数都不超过1,000,000,000

（2）20%的数据2<=a,b<=100,n<=a,n<=b,n<=10

（3）100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100

题解

要求出一个方块内的极值，我们不妨维护两次单调队列：

  • 第一次：行，单调队列
  • 第二次：上面那个单调队列得到的结果按列维护

这样我们就可以达到目的了

图片@ｃｈｉｌｌ（洛谷）:

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>

using namespace std;

const int maxn = 1005;

int a, b, n;
struct node { int val, pos; } q[maxn];
int map[maxn][maxn];
int min_val[maxn][maxn], max_val[maxn][maxn];
int min_ans[maxn][maxn], max_ans[maxn][maxn];

int main() {
	cin >> a >> b >> n;
	for (int i = 1; i <= a; i ++)
		for (int j = 1; j <= b; j ++)
			cin >> map[i][j];
	int head = 0, tail = 0;
	// row max
	for (int i = 1; i <= a; i ++) {
		head = 0, tail = 0;
		for (int j = 1; j <= b; j ++) {
			while (head < tail && map[i][j] >= q[tail - 1].val) tail --;
			q[tail ++] = (node) { map[i][j], j };
			while (head < tail && j - q[head].pos + 1 > n) head ++;
			if (j >= n) max_val[i][j - n + 1] = q[head].val; 
		}
	}
	// row min
	for (int i = 1; i <= a; i ++) {
		head = 0, tail = 0;
		for (int j = 1; j <= b; j ++) {
			while (head < tail && map[i][j] <= q[tail - 1].val) tail --;
			q[tail ++] = (node) { map[i][j], j };
			while (head < tail && j - q[head].pos + 1 > n) head ++;
			if (j >= n) min_val[i][j - n + 1] = q[head].val; 
		}
	}

	for (int j = 1; j <= b - n + 1; j ++) {
		head = 0, tail = 0;
		for (int i = 1; i <= a; i ++) {
			while (head < tail && max_val[i][j] >= q[tail - 1].val) tail --;
			q[tail ++] = (node) { max_val[i][j], i };
			while (head < tail && i - q[head].pos + 1 > n) head ++;
			if (i >= n) max_ans[i - n + 1][j] = q[head].val;
		}
	}
	for (int j = 1; j <= b - n + 1; j ++) {
		head = 0, tail = 0;
		for (int i = 1; i <= a; i ++) {
			while (head < tail && min_val[i][j] <= q[tail - 1].val) tail --;
			q[tail ++] = (node) { min_val[i][j], i };
			while (head < tail && i - q[head].pos + 1 > n) head ++;
			if (i >= n) min_ans[i - n + 1][j] = q[head].val;
		}
	}
	
	int ans = 2e9;
	for (int i = 1; i <= a - n + 1; i ++)
		for (int j = 1; j <= b - n + 1; j ++)
			ans = min(ans, max_ans[i][j] - min_ans[i][j]);
	
	cout << ans << endl;
	
	return 0;
}

发表于 分类于 Disqus：
本文字数： 1.3k 阅读时长 ≈ 1 分钟
博客园 同步已开启

题目

题目描述

给定一行n个非负整数a[1]..a[n]。现在你可以选择其中若干个数，但不能有超过k个连续的数字被选择。你的任务是使得选出的数字的和最大。

输入格式

第一行两个整数n，k

以下n行，每行一个整数表示a[i]。

输出格式

输出一个值表示答案。

输入输出样例

输入 #1 
5 2
1
2
3
4
5
输出 #1 
12

说明/提示

对于20%的数据，n <= 10

对于另外20%的数据， k = 1

对于60%的数据，n <= 1000

对于100%的数据，1 <= n <= 100000，1 <= k <= n，0 <= 数字大小 <= 1,000,000,000

时间限制500ms

题解

我们要选出和最大的一堆数，但是这非常难，所以我们可以考虑怎么做才能删除最少的数。设$f[i]$表示删除第$i$个数的最小和，那么$f[i]$可以由前$k+1$个$f$转移而来（因为是不超过$k$个），即以下转移方程给出：

观察后半段，其实就是个单调队列，直接维护就行了。最后的答案：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#define int long long

using namespace std;

const int maxn = 100005;
int n, k, f[maxn], a[maxn];
struct node { int val, pos; } q[maxn];

signed main() {
	cin >> n >> k;
	f[0] = 0;
	int head = 0, tail = 1, sum = 0;
	// min -> increase
	q[head] = (node) { f[0], 0 };
	for (int i = 1; i <= n; i ++) {
		cin >> a[i];
		sum += a[i];
		f[i] = a[i] + q[head].val;	
		while (head < tail && f[i] <= q[tail - 1].val) tail --;
		q[tail ++] = (node) { f[i], i };
		while (head < tail && i - q[head].pos + 1 > k + 1) head ++;
	}
//	for (int i = 0; i <= n; i ++) cout << f[i] << " ";
//	cout << endl; 
	int ans = 8e18;
	for (int i = n - k; i <= n; i ++) ans = min(ans, f[i]);
	cout << sum - ans << endl;
	return 0;
}

注意

十年OI一场空，不开longlong见祖宗。